Unit III Lesson 1 Ex2
Ex2. y’’+9y=0 and we know the solution y1=sin(3x). Find a second linearly independent solution.
Solution1:
Ex2. y’’+9y=0 and we know the solution y1=sin(3x). Find a second linearly independent solution.
Solution1:
We first assume that y2 = u(x)sin(3x), and differentiating y2, we get y2’=3u(x)cos(3x)+u’(x)sin(3x) and second derivative
y2’’=-9u(x)sin(3x)+3u’(x)cos(3x)+3u’(x)cos(3x)+u’’(x)sin(3x).
This simplifies to y2’’=-9u(x)sin(3x)+6u’(x)cos(3x)+ u’’(x)sin(3x) with a little algebra.
Substitution this y2 into our equation y’’+ 9y=0 gives the following equation:
u’’(x)sin(3x)+6u’(x)cos(3x) -9u(x)sin(3x)+9u(x)sin(3x)=0 and simplifying that yields:
u’’(x)sin(3x)+6u’(x)cos(3x)=0.
Now let w(x)=u’(x) and we get w’(x)sin(3x)+6w(x)cos(3x)=0, and
dividing by w(x)sin(3x) we
get
, which when
integrated give
, simplifying
to
and now u(x)=
the integral of w(x) or
or
and letting
C1=0 and C= -3 we get u(x)=cot(3x).
Therefore y2=u(x)y1=cot(3x)sin(3x) so we have y2=cos(3x).
A fundamental set is {sin(3x), cos(3x)}
and the general solution is y=C1sin(3x)+C2cos(3x).
Solution 2:
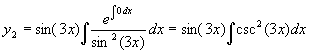, so we have
y2=sin(3x)(cot(3x)+C) and if we let C=0, we have y2=cos(3x)
Comment: Yes, it was easier this way, but you should try to follow solution1 given above to see the process, not just the ‘formula’.