Unit III Lesson 1

Reduction of order as multiplying a known solution by some function and then finding the function and examples.
Another example of using reduction of order.
Look at another example of reduction of order.

If we already know a solution to a DE, can we find a second linearly independent solution using the first?

Let’s assume we know a solution y₁. Recall a linearly independent solution will be such that our second solution y₂ cannot be a constant multiple of y₁. Therefore assume that y₂=u(x)y₁ where u(x) is not a constant function. This is a little like ‘variation of parameters’ from Unit I Lesson 7. Here is a procedure that should work in the general case.

The generalized second order linear homogeneous equation can be written y’’+P(x)y’+Q(x)y=0 and we suppose that we know the solution y₁. 

We define the function y=u(x)*y₁(x) and note its first and second derivatives are

y’=uy₁’+ y₁u’ and y’’=uy₁’’+ 2u’y₁’+ y₁u’’. 

Substitution into y’’+P(x)y’+Q(x)y=0 ,we get this expression:

(uy₁’’+2u’y₁’+y₁u’’) +P(x)( uy₁’+y₁u’) + Q(x)uy₁ = 0

which with a little algebra can be written:

u(y₁’’+P(x)y₁’+Q(x)y₁)+u’(2y₁’+P(x)y₁)+u’’y₁=0. 

Since y₁ is a solution of the homogeneous equation, the colored expression, y₁’’+P(x)y₁’+Q(x)y₁, must be 0.

This simplifies the expression to u’’y₁+u’(2y₁’+P(x)y₁)=0.

 If we let w=u’ (and w’=u’’), this reduces the order of the DE we must solve to first order.

It becomes w’y₁+w(2y₁’+P(x)y₁)=0 and dividing both sides of this by wy₁ we get.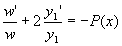

Now integrating both sides, we find , and upon making both sides exponents for e,, which when solving for w, yields.

Recall w = u’, so we can integrate this expression to find u:.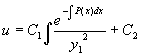

Constants shouldn’t affect our linearly independent solution, so let's assign C₁=1 and C₂=0. Then we will get .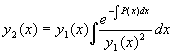

This is probably not as bad as it looks, so let’s try to solve some example problems.

Take the link after trying it yourself. 

Take this link after you’ve tried it yourself.