 or
or
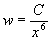 , therefore we
get u=C1x-5+C2.
, therefore we
get u=C1x-5+C2.
Ex3. x2y’’+2xy’-6y=0 with given solution y1=x2

First assume y2=ux2, and y2’=2ux+u’x2 and y2’’=u’’x2+4u’x+2u.
Substituting into x2y’’+2xy’-6y=0 we get x2(u’’x2+4u’x+2u)+2x(2ux+u’x2)-6y=0 and simplifying by adding
like terms we get: u’’x4+6u’x3=0.
We reduce the order by w=u’ to get
w’x4+6wx3=0. Now dividing by wx4 and rearranging, we get
![]() and integrating
both sides,
and integrating
both sides,![]()
 or
or
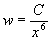 , therefore we
get u=C1x-5+C2.
, therefore we
get u=C1x-5+C2.
If we let C1=1, C2=0 we get u=x-5, hence our second solution y2=x2x-5=x-3.
Our fundamental set is {x2,x-3}and the general solution is y=C1x2+C2x-3
Rewrite x2y’’+2xy’-6y=0 (dividing by x2)
as![]() ,
,
and so use the formula to get
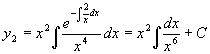 .
.
If we let the C=0, we get y2=x-3
