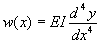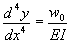Ex1. A beam of length L is embedded at both ends, and the constant load w₀ is uniform along its length. (I.e. w(x)=w₀ for all x in the interval 0<x<L. Find the function representing the deflection of the beam.

Solution:

Solving the DE 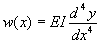is easy enough, it just requires iterated integration after dividing both sides by EI to get :

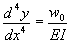Note that I used C₁, and C₂ to absorb the fractions, and didn’t bother to rename them, since they were always arbitrary.

The boundary conditions y(0)=0, y’(0)=0 forces both C₄ and C₃ both to be zero, and our solution becomes with . Note here that the C_i are arbitrary, but a relation between the function and its derivative must be maintained.

The boundary conditions y(L)=0, y’(L)=0 gives the system of equations

which can be solved for C₁and C₂ using Cramer’s Rule (See Unit III lesson 5).

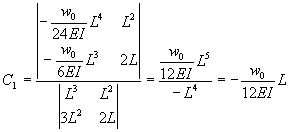
Finally, we get the equation of the deflection to be the quartic equation:

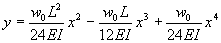
If we let L=1, and assume w₀=24EI to simplify this, we get the graph:

Our interest is in the interval between 0 and 1. Recall that the graph is showing positive y direction as up, but in our example we assumed it was down. The beam’s deflection is really as this diagram shows:

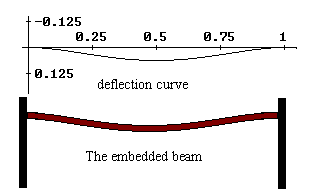
Note that this is a little bit of a drastic deflection, but conditions here are illustrative, not necessarily reality based. Besides, I didn't give a unit of measure, so suppose L was 1 rod.