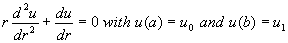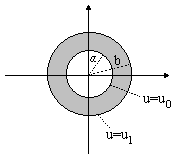
Ex3. The temperature u(r) in the circular ring shown below is determined from the boundary value problem: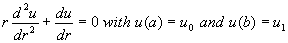 for u₀ and u₁ constants.

Show that

Solution:

If we multiply both sides by r, we have a Cauchy-Euler equation (see unit III lesson 6), so assuming a solution of form u=r^m, u’=mr^m-1, u’’=m(m-1)r^m-2, we get the characteristic equation r²m(m-1)r^m-2+rmr^m-1=0. Factoring out r^m and simplifying, we get r^m(m²-m+m)=0. The solution is m=0 as a double root, hence the solution is u=C₁+C₂ln(r). The boundary conditions yield the system

Using Cramer’s rule we get the solutions:

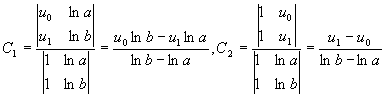
Now the solution to the BVP is:

.

This simplifies to

QED