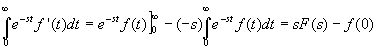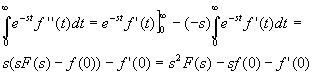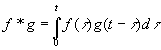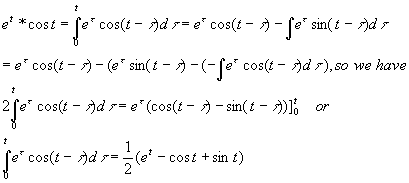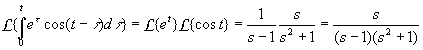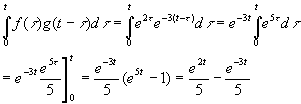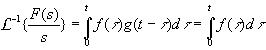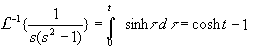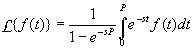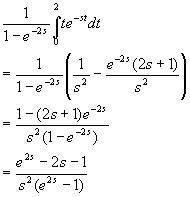Unit V Lesson 4
Additional operational properties: derivatives, convolutions,
transform of an integral, periodic functions
Derivatives of transforms or transforms of products of powers of t.
Examples, one of them done two ways.
Second order equation done without partial fractions.
Convolution of functions, inverse transforms of products, an example.
Transforms of periodic functions.
Transform of sin(t) as a transform of a periodic function.
In order to solve differential equations with transforms, we need to know
how to transform functions f(t), f ’(t), f ’’(t),… to
the algebra domain. These transforms are fairly straightforward.

If we know L{f(t)}=F(s) and desire
to find L{f ’(t)}, we can just
evaluate the integral using integration by parts: u=e-st, dv=f
'(t)dt, du=-se-stdt, v=f(t).
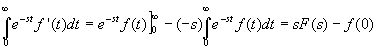

If we desire L{f ’’(t)},
we can again use integration by parts: u=e-st, dv=f ''(t)dt,
du=-se-stdt, v=f '(t) and get the following result:
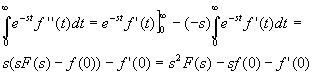
The general case follows:
Theorem Transform of a derivative
If f(t), f '(t), f "(t), …,f(n-1)(t) are
continuous on the interval [0,infinity) and are of exponential order and
if f(n)(t) is piecewise continuous on [0,infinity), then
L{f(n)(t)}=snF(s)-sn-1f(0)-sn-2f
'(0)- …-f(n-1)(0) where
L{f(t)}=F(s).

Example
Find the transform of the equation
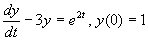
Solution:
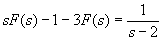 .
.

We can then solve the equation for F(s), perform the inverse transform on
F(s), and we have the solution to the IVP. Compare with Unit I section 7
where we solved with an integrating factor.
Convolution
The convolution gives a way to find inverse transforms of products of functions
in the algebra domain. 
Def: Convolution
If f and g are piecewise continuous on the interval
[0,infinity) then the convolution of f and g, denoted f*g, is given
by the integral: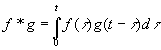

Example
The convolution of f(t)=et and g(x)=cost
is
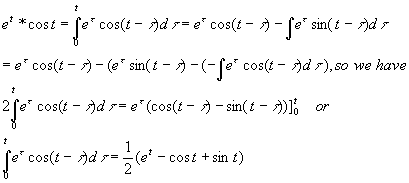

Theorem Convolution theorem
If f and g are piecewise continuous on the interval [0,infinity) and of
exponential order, then
L{f(t)*g(t)}=
L{f(t)}L{g(t)}=F(s)G(s)
Proof is in the textbook. 
Example
Find
L{et*cost}
By the convolution theorem,
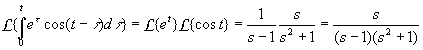

You can probably guess that this is not the useful stuff about convolutions,
but this should be useful:
Inverse form of the convolution theorem
L-1{F(s)G(s)}=f(t)*g(t)
In other words, if we wish to find the inverse transform of a product, we
can use the convolution of the inverse transforms.

Example
Find
L-1{1/[(s-2)(s+3)]}
Solution:
Yes we could use partial fractions, but try the inverse form of the convolution
theorem:
F(s)=1/(s-2), G(s)=1/(s+3) so since we know
L-1{F(s)}=e2t
and
L-1{G(s)}=e-3t,
we can say
L-1{1/[(s-2)(s+3)]}=
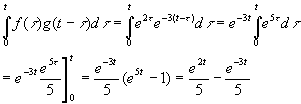

Transform of an integral
If g(t)=1, then L{g(t)}=G(s)=1/s.
The convolution theorem would then force the transform of the integral
of f(t) to be F(s)G(s)=F(s)/s, or more importantly, in inverse form,
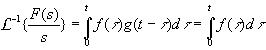

Example
Find the inverse transform:
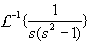
Solution:
Since the inverse transform of 1/(s2-1) is cosht, we have
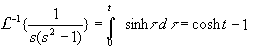
Ex1. Find the inverse transform:
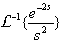
Take this link after trying it yourself.
Transform of a periodic function
Periodic functions are common mathematical models of periodically applied
forces from either forcing functions in mechanics or electrical forces. If
a periodic function has period P>0, then f(t+P)=f(t) by definition of
'periodic'.
Theorem Transform of a periodic
function
If f(t) is piecewise continuous on [0,infinity) and periodic
with period P, then the Laplace transform of f(t) is given by
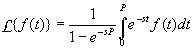
Proof:
The proof comes from the definition of Laplace transform.


Example
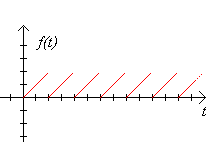
Find the transform of the sawtooth function:
Solution:
On the interval [0,2), we have f(t)=t and the function is periodic with period
P=2, since f(t+2)=f(t) for every t.
Therefore L{f(t)}=
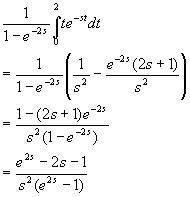

I’ll admit, I relented and used a CAS (Derive) to get the last result,
because I don’t trust myself not to err!
You try this one:
Ex2.
Find the transform of the equation:
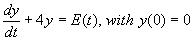
where E(t) is the periodic function in the graph:

Take this link after you transform the DE. Don't
try to solve this one, that's in the next section!.
****assignment****
Chapter 7 section 4
1,7,15,21,29,31